Jinhyuk Kim

Software Development Engineer @ Amazon

reniowood at gmail.com

resume

BOJ 3938 - Concert Hall Scheduling

2018-09-21

최종 수정일: 2021-06-26

1년 365일 두 개의 콘서트 홀을 운영하면서 예약 요청 일정과 금액이 주어졌을 때 얻을 수 있는 가장 큰 금액을 묻는 문제이다. 언뜻 보았을 때는 각 예약과 일정을 이분 그래프로 나타낸 후 최소 비용 최대 유량 알고리즘을 사용하면 될 것으로 생각했다. 네트워크 유량 문제가 다 그렇지만 이 문제도 그래프 모델링이 매우 중요하다.

우리가 최대로 만들어야 하는 유량은 곧 예약 숫자이기 때문에 예약을 네트워크에 흐르도록 만들어야 한다. 처음 생각했던 방식으로는 n개의 예약과 365개의 날짜를 예약을 나타내는 간선을 통해 연결해 이분 그래프를 만들어야 한다. 하지만 이렇게 하면 어떻게 해도 예약 일정 하나는 시작일부터 종료일까지 하나의 홀만 사용하고, 부분 예약은 되지 않는다는 제약 조건은 만족할 수 없다.

문제 풀이의 핵심은 아래 예제 데이터에 대해 다음과 같이 유량 네트워크를 모델링하는 것이다.

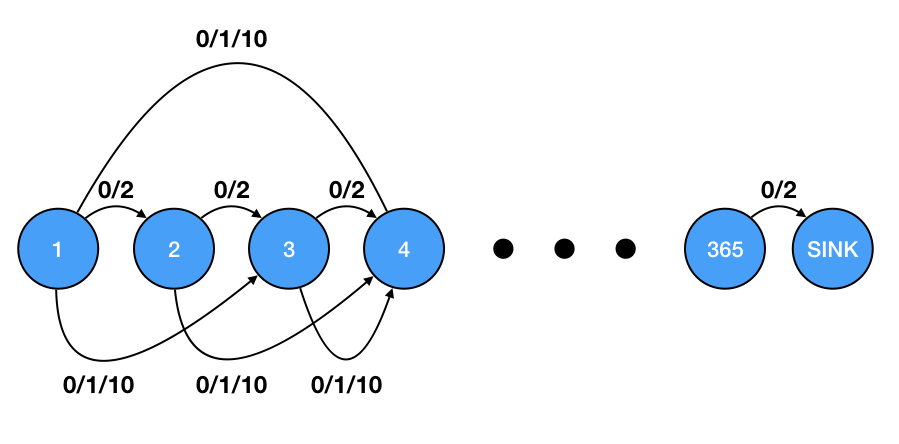
한 번에 최대 두 개의 콘서트 홀에 예약이 가능하므로 1일부터 365일까지 차례대로 용량이 2인 간선으로 연결한다. 그리고 각 예약마다 시작일 정점에서 종료일 다음 날 정점까지 연결하는 용량 1, 비용이 요금에 -1을 곱한 값인 간선을 추가한다. 종료일 정점으로 연결하게 되면 시작일과 종료일이 같은 예약이나 한 예약의 종료일과 다른 예약의 시작일이 같은 것을 처리할 수 없다. 따라서 366일에 대응되는 정점도 추가해야 하며, 끝 정점은 366일 다음 정점이 된다. 최대 비용을 구해야 하므로 비용도 요금에 -1을 곱한 값을 사용한다.

위 네트워크에 최소 비용 최대 유량 알고리즘을 적용한 소스코드는 다음과 같다. 같은 기간에 대한 예약이 여러 번 들어올 수 있으므로 행렬을 이용한 그래프가 아닌 인접 간선을 이용한 그래프를 만들어야 한다. 또한 최대 비용을 구해야 하므로 최소 비용을 구한 결과에 -1을 곱해주어야 하는 것을 잊지 말아야 한다.

import java.io.*;
import java.util.*;

public class Main {
    private static final int NUM_DAYS = 365;
    private static final int SOURCE = 0, SINK = NUM_DAYS + 1;

    private static class Edge {
        int from, to, capacity, cost;
        Edge reverse;

        public Edge(int from, int to, int capacity, int cost) {
            this.from = from;
            this.to = to;
            this.capacity = capacity;
            this.cost = cost;
        }
    }

    private static void addEdge(Map<Integer, List<Edge>> network, Edge edge) {
        List<Edge> edges = network.getOrDefault(edge.from, new ArrayList<>());
        edges.add(edge);
        network.put(edge.from, edges);
    }

    private static void createNetwork(int n, int[][] applications, Map<Integer, List<Edge>> network) {
        for (int i = 0; i < NUM_DAYS + 1; ++i) {
            Edge edge = new Edge(i, i + 1, 2, 0);
            Edge reverse = new Edge(i + 1, i, 0, 0);
            edge.reverse = reverse;
            reverse.reverse = edge;
            addEdge(network, edge);
            addEdge(network, reverse);
        }

        for (int i = 0; i < n; ++i) {
            int[] application = applications[i];

            Edge edge = new Edge(application[0], application[1] + 1, 1, -application[2]);
            Edge reverse = new Edge(application[1] + 1, application[0], 0, application[2]);
            edge.reverse = reverse;
            reverse.reverse = edge;
            addEdge(network, edge);
            addEdge(network, reverse);
        }
    }

    private static List<Edge> findMinCostPath(int networkSize, Map<Integer, List<Edge>> network) {
        Edge[] parents = new Edge[networkSize];
        Queue<Integer> queue = new LinkedList<>();
        boolean[] isInQueue = new boolean[networkSize];
        int[] distances = new int[networkSize];
        Arrays.fill(distances, Integer.MAX_VALUE);

        queue.offer(SOURCE);
        isInQueue[SOURCE] = true;
        distances[SOURCE] = 0;

        while (!queue.isEmpty()) {
            int curr = queue.poll();
            isInQueue[curr] = false;

            if (network.containsKey(curr)) {
                for (Edge edge : network.get(curr)) {
                    int next = edge.to;
                    if (edge.capacity > 0 && distances[curr] + edge.cost < distances[next]) {
                        distances[next] = distances[curr] + edge.cost;
                        parents[next] = edge;

                        if (!isInQueue[next]) {
                            queue.offer(next);
                            isInQueue[next] = true;
                        }
                    }
                }
            }
        }

        List<Edge> edges = new ArrayList<>();
        for (int node = SINK; parents[node] != null; node = parents[node].from) {
            edges.add(parents[node]);
        }

        return edges;
    }

    private static long findMinCostMaxFlow(int networkSize, Map<Integer, List<Edge>> network) {
        long minCost = 0;

        while (true) {
            List<Edge> edges = findMinCostPath(networkSize, network);

            if (edges.isEmpty()) {
                break;
            }

            long flow = Long.MAX_VALUE;
            for (Edge edge : edges) {
                flow = Math.min(flow, edge.capacity);
            }

            for (Edge edge : edges) {
                minCost += flow * edge.cost;
                edge.capacity -= flow;
                edge.reverse.capacity += flow;
            }
        }

        return minCost;
    }

    private static long solve(int n, int[][] applications) {
        int networkSize = NUM_DAYS + 2;
        Map<Integer, List<Edge>> network = new HashMap<>();

        createNetwork(n, applications, network);

        return -findMinCostMaxFlow(networkSize, network);
    }

    public static void main(String[] args) throws IOException {
        BufferedReader in = new BufferedReader(new InputStreamReader(System.in));

        while (true) {
            int n = Integer.parseInt(in.readLine());

            if (n == 0) {
                break;
            }

            int[][] applications = new int[n][3];

            for (int i = 0; i < n; ++i) {
                StringTokenizer st = new StringTokenizer(in.readLine());

                applications[i][0] = Integer.parseInt(st.nextToken()) - 1;
                applications[i][1] = Integer.parseInt(st.nextToken()) - 1;
                applications[i][2] = Integer.parseInt(st.nextToken());
            }

            System.out.println(solve(n, applications));
        }

        in.close();
    }
}

2021-06-26 추가: 해당 문제 제출 답안이 데이터 추가 이후 틀린 것으로 확인되어, 제대로 풀지 못하던 경우인

시작일과 종료일이 같은 예약이 두 개 이상 있을 경우
1일부터 365일까지의 예약이 두 개 이상 있을 경우

를 대응하기 위해 설명을 수정했습니다.