Jinhyuk Kim

Software Development Engineer @ Amazon

reniowood at gmail.com

resume

BOJ 10786 - Catering

2018-09-26

참고: 해당 풀이는 전명우님의 블로그의 글 ACM ICPC World Finals 2015에서 많은 도움을 받았습니다. 감사합니다.

k개의 팀이 n개의 요청을 처리하기 위해 각 팀에 0개 이상의 요청을 할당한다. 각 팀은 요청을 처리하기위해 회사에서 물품을 들고 출발해 요청한 장소를 순회하고 회사로 돌아온다. 모든 요청 장소에 대해 한 요청 장소에서 다른 요청 장소로 물품을 옮기는 비용이 주어졌을 때, 모든 요청을 처리할 수 있는 가장 작은 비용을 알아내야 한다.

문제를 읽고 나니 팀 정점과 요청 정점으로 이분 그래프를 만들어 유량 네트워크로 변환해 최소 비용 최대 유량 문제를 풀면 되겠다는 생각은 쉽게 떠올랐다. 하지만 ‘어떻게 모든 요청을 처리하도록 강제하는가’는 매우 어려운 문제였다. 각 요청을 한 번만 처리하도록 하기 위해 요청 정점을 두 정점으로 쪼개는 것 이외의 처리가 필요했다.

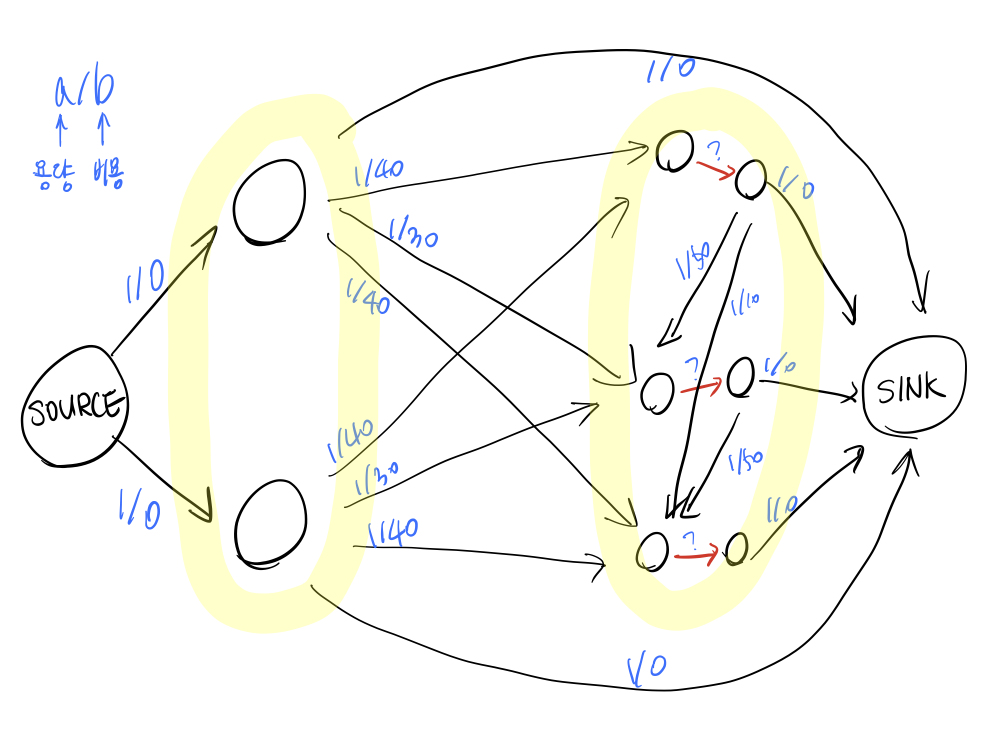
오랫동안 고민해 보았지만 쉽게 떠오르지 않았고, 결국 웹 검색을 통해 전명우님의 블로그 글에 해설과 소스 코드가 있어 읽어보고 풀 수 있었다. 다만 내가 처음 생각했던 네트워크와는 조금 다른 모양으로 구성한 해설이 있어 내 방식대로 조금 바꾸어 다시 풀어보았다.

모든 요청을 처리하도록 강제하는 방법은 요청 정점을 쪼갠 두 정점 사이의 간선에 다른 비용에 비해 매우 작은 음수값(가령 -1e10)의 비용을 할당하는 것이었다. 이렇게 되면 유량이 흐르는 한 반드시 해당 간선들을 방문할 수밖에 없고, 따라서 모든 요청 정점을 방문하게 된다. 다만 마지막 정답에서 해당 음수값에 요청 갯수를 곱해서 빼주어야 실제 정답을 얻을 수 있다.

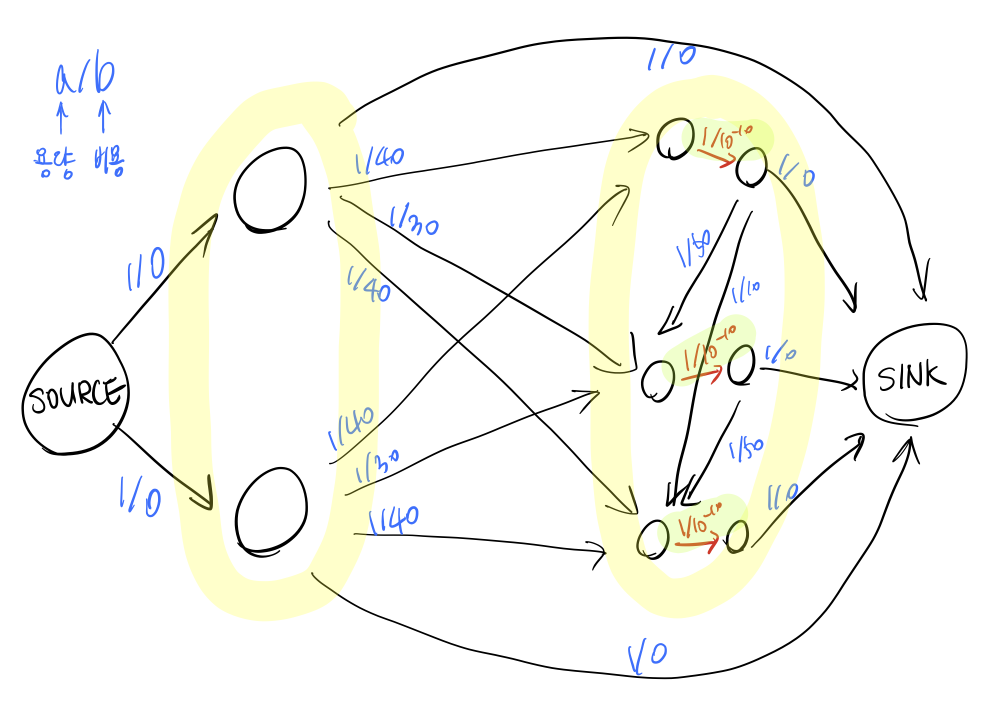
다음 소스 코드는 위의 유량 네트워크 모델링으로 작성한 소스 코드이다.

import java.io.*;
import java.util.*;

public class Main {
    private final int SOURCE = 0, SINK = 1, BASE = 2;
    private final long MIN_COST = (long) -1e10;

    private class Edge {
        int u, v, capacity, flow;
        long cost;
        Edge rev;

        public Edge(int u, int v, int capacity, long cost) {
            this.u = u;
            this.v = v;
            this.capacity = capacity;
            this.flow = 0;
            this.cost = cost;
            this.rev = null;
        }
    }

    private int n, k;
    private int[][] costs;
    
    private int networkSize;
    private List[] network;

    public Main(int n, int k, int[][] costs) {
        this.n = n;
        this.k = k;
        this.costs = costs;
    }

    private void addEdge(int from, int to, int capacity, long cost) {
        Edge edge = new Edge(from, to, capacity, cost);
        Edge reverseEdge = new Edge(to, from, 0, -cost);
        edge.rev = reverseEdge;
        reverseEdge.rev = edge;
        network[from].add(edge);
        network[to].add(reverseEdge);
    }

    private int teamNode(int i) {
        return BASE + i;
    }

    private int requestInNode(int i) {
        return BASE + k + i;
    }

    private int requestOutNode(int i) {
        return BASE + k + n + i;
    }

    private void createNetwork() {
        for (int i = 0; i < k; ++i) {
            addEdge(SOURCE, teamNode(i), 1, 0);
            addEdge(teamNode(i), SINK, 1, 0);
        }

        for (int i = 0; i < n; ++i) {
            addEdge(requestOutNode(i), SINK, 1, 0);
        }

        for (int i = 0; i < n; ++i) {
            addEdge(requestInNode(i), requestOutNode(i), 1, MIN_COST);
        }

        for (int i = 0; i < k; ++i) {
            for (int j = 0; j < n; ++j) {
                addEdge(teamNode(i), requestInNode(j), 1, costs[0][j]);
            }
        }

        for (int i = 0; i < n - 1; ++i) {
            for (int j = i + 1; j < n; ++j) {
                addEdge(requestOutNode(i), requestInNode(j), 1, costs[i + 1][j]);
            }
        }
    }
    
    private Edge[] findMinCostPath() {
        Edge[] edges = new Edge[networkSize];
        Queue<Integer> queue = new LinkedList<>();
        boolean[] isInQueue = new boolean[networkSize];
        long[] distances = new long[networkSize];
        Arrays.fill(distances, Long.MAX_VALUE);

        queue.offer(SOURCE);
        isInQueue[SOURCE] = true;
        distances[SOURCE] = 0;

        while (!queue.isEmpty()) {
            int curr = queue.poll();
            isInQueue[curr] = false;

            for (Edge edge : (List<Edge>) network[curr]) {
                int next = edge.v;

                if (edge.capacity > edge.flow && distances[curr] + edge.cost < distances[next]) {
                    distances[next] = distances[curr] + edge.cost;
                    edges[next] = edge;

                    if (!isInQueue[next]) {
                        queue.offer(next);
                        isInQueue[next] = true;
                    }
                }
            }
        }

        return edges;
    }

    private long findMinCostMaxFlow() {
        long minCost = 0;

        while (true) {
            Edge[] edges = findMinCostPath();

            if (edges[SINK] == null) {
                break;
            }

            int flow = Integer.MAX_VALUE;
            for (Edge edge = edges[SINK]; edge != null; edge = edges[edge.u]) {
                flow = Math.min(flow, edge.capacity - edge.flow);
            }

            for (Edge edge = edges[SINK]; edge != null; edge = edges[edge.u]) {
                minCost += flow * edge.cost;
                edge.flow += flow;
                edge.rev.flow -= flow;
            }
        }

        return minCost;
    }

    public int solve() {
        networkSize = BASE + k + 2 * n;
        network = new List[networkSize];
        for (int i = 0; i < networkSize; ++i) {
            network[i] = new ArrayList<Edge>();
        }

        createNetwork();

        return (int) (findMinCostMaxFlow() - n * MIN_COST);
    }

    public static void main(String[] args) throws IOException {
        BufferedReader in = new BufferedReader(new InputStreamReader(System.in));

        StringTokenizer st = new StringTokenizer(in.readLine());

        int n = Integer.parseInt(st.nextToken());
        int k = Integer.parseInt(st.nextToken());

        int[][] costs = new int[n][n];

        for (int i = 0; i < n; ++i) {
            st = new StringTokenizer(in.readLine());

            for (int j = i; j < n; ++j) {
                costs[i][j] = Integer.parseInt(st.nextToken());
            }
        }

        System.out.println(new Main(n, k, costs).solve());

        in.close();
    }
}